[Dreamhack] Dream Beginner_Virtual Machine/ Fundamentals of Computer Science

1. 가상 환경 구축

호스트 머신: 실제 컴퓨터를 의미

게스트 머신: 호스트 머신 위에서 돌아가는 VM

-> 호스트 머신 위에서 돌아가는 VM을 게스트 머신이라고 부른다.

 

  VM 소프트웨어를 사용하면 하나의 호스트 머신에서 여러 개의 가상 머신을 동시게 실행할 수 있기 때문에 물리적인 서버를 여러대 구입하는 것보다 경제적이다.

 

 

 

 

 

2. 컴퓨터 과학 챕터에 들어가며

  컴퓨터 과학(Computer Science)은 컴퓨터를 이용한 모든 작업과 그 기반 이론을 연구하는 학문이다. 해킹은 이러한 컴퓨터 과학 지식을 응용하여, 프로그램이나 시스템의 취약점을 발견하고 공격하는 행위를 가리킨다. 따라서 컴퓨터 시스템, 네트워크, 프로그래밍 언어, 운영 체제 등의 컴퓨터 과학 지식이 요구된다.

  컴퓨터 과학을 깊게 알아만 해킹을 배울 수 있다는 말은 아니다. 하지만 컴퓨터 과학에 대한 기본적인 지식 없이는 해킹을 효과적으로 수행하는 것은 불가능하다. 해킹과 컴퓨터 과학이 밀접하게 연관되어 있음을 기억하고, 차근차근 공부해 나가자.

 

 

 

 

 

 

3. 진법

  진법은 임의의 숫자 혹은 문자를 사용하여 수를 표현하는 체계를 말한다. n진법은 한 자릿수를 n가지(0~n)의 숫자 혹은 문자로 나타낼 수 있다. 오늘은 10진법(decimal), 2진법(binary), 16(hexadecimal)진법을 배워보자.

 

 

 

3-1) 10진법: 10개(0~9)의 숫자로 수를 표현한다

  실생활에서 사람들이 자연스럽게 사용하고 있는 수 체계이다.

 

 

 

3-2) 2진법: 2개(0,1)의 숫자로 수를 표현한다

  컴퓨터는 2진법을 사용한다. 컴퓨터가 0과 1로 이루어진 세상이라고 불리는 이유이다. 전적 신호의 ON/ OFF 상태를 1과 0으로 표현하고, 이러한 0과 1의 조합으로 이루어진 비트(bit)가 모여서 데이터를 표현한다.

  이진수를 표현할 때, 0b라는 접두어를 붙인다. 예를들어 0b1110 = 10진수 14이다.

 

 

3-3) 16진법: 16개(0~9,A~F)의 문자로 수를 표현한다.

  2진법은 수가 조금만 커져도 표현할 때 많은 글자 수가 필요하여 비효율적이고, 가독성 또한 떨어진다. 따라서 2진수를 조금 더 간편하고 효율적으로 표현하기 위해 다른 진법으로 표현할 필요가 있는데, 그중에서 16진법이 2진수의 대체제로 많이 사용된다. 0x라는 접두어를 붙인다.

  2진수 4자리는 16진수 한 자리로 축약하여 표현할 수 있다. 예를들어 0b1100 = 0xC로 나타낼 수 있다.

 

  16진수는 컴퓨터 곳곳에서 활용되는 진법이다. 디버깅 도구 같은 경우, 일반적으로 메모리의 위치를 나타내는 주소값을 16진수 형태로 출력한다. 해킹을 공부하다 보면 16진수 형태의 데이터를 접하는 일이 굉장히 빈번하기 때문에 익숙해지기를 바란다.

 

2^5=16

 

 

 

 

 

 

4.비트(bit)와 바이트(byte)

  bit와 byte는 컴퓨터의 데이터를 다루는 데 가장 기본이 되는 개념이다. 컴퓨터는 0과 1만으로 데이터를 표현하고 처리한다. 이때 0과 1을 나타내는, 컴퓨터에서 사용하는 데이터의 최소 단위를 1비트(1bit)라고 한다

  8개의 bit로 구성된 더 큰 단위를 1바이트(byte)라고 하며, 이는 메모리에 저장되는 최소 단위이다. 1byte는 2^8=256가지의 수를 표현할 수 있다. 10진수로 0~255, 2진수로 00000000~11111111, 16진수로 00~FF까지 나타낸다(2진수 4자리->16진수 1자리)

 

  자꾸 헷갈리는데, 2진수와 16진수의 관계 잘 파악해야 할 것 같다. 0b11111111 = 0xFF(4 bit씩 끊어서 해석한다고 생각)

  예시와 함께 이해하자. 2진수=32+16+8+4=60 / 16진수=16*3+12/ 10진수=60

 

 

 

 

 

 

4-1) 최상위 비트(MSB), 최하위 비트(LSB)

  여러 개의 비트로 구성된 이진 데이터에서 가장 왼쪽에 있는 비트를 Most Significant Bit(MSB)라고 하고, 가장 오른쪽에 있는 비트를 Least Significant Bit(LSB)라고 한다. 가장 왼쪽에 있는 비트가 숫자의 크기에 가장 큰 영향을 미치기 때문에 가장 중요한 비트라고 부르는 것이며, 최하위 비트도 이런 방식으로 이해하면 된다.

  예를들어 '0b10010100에서 MSB는 1이고, LSB는 0이다'라고 말할 수 있다. 

 

 

 

 

 

4-2) 부호 비트

 

  부호가 있는 데이터(Signed Data)의 경우, MSB는 부호(+/ -)의 의미를 가지게 된다. MSB가 0이면 양수, 1이면 음수를 나타낸다.

  예를들어 0b10010100이 부호가 있는 데이터라면, MSB가 1이기 때문에 10진수로 나타내면 -108이 된다[2의 보수법 사용: 비트 반전=01101011 ->1을 더함=01101100 -> 4+8+32+64]. 반면 부호가 없는 데이터일 경우 2의 보수법 사용 없이 양수 148이 된다[그냥 4+16+128]

 

  부호가 있는 데이터와 부호가 없는 데이터를 구분하는 것은 비트 패턴만으로는 알 수 없다. 데이터가 어떻게 사용될지를 기반으로 구분해야한다. 주로 주석을 통해 부호 여부를 알려준다.

 

 

 

 

4-3) 부호가 있는 데이터/ 부호가 없는 데이터 상세 설명

  부호가 있는 데이터는 양수와 음수 모두를 표현할 수 있다. 부호가 있는 데이터를 표현하는 방법 중 가장 일반적인 것은 2의 보수법이며, 2의 보수법을 사용함으로써 덧셈과 뺄셈 연산을 동일한 하드웨어 회로에서 수행할 수 있다는 효율성을 가진다.(4bit 예시에서 데이터의 범위: 0000~0111=0~7/ 1111~1000=-1 ~ -8)

 

 

  부호가 없는 데이터는 오직 양수만을 표현한다. 모든 비트가 숫자 값 자체를 나타내는 것이다. 따라서 같은 비트 수를 사용하더라도, 부호가 있는 데이터보다 더 큰 양수를 표현할 수 있다.

 

 

 

4-4) 2의 보수 표현법

1. 해당 수의 모든 비트를 반전시킨다
2. 그 결과에 1을 더한다

 

 

 

 

 

 

 

 

5. 바이트 오더링(Byte Ordering)

  컴퓨터는 데이터를 메모리에 저장할 때 바이트 단위로 나눠서 저장한다. 컴퓨터가 저장하는 데이터는 32비트(4바이트) 또는64비트(8바이트)로 구성된다. 컴퓨터는 연속되는 데이터를 바이트 단위로 순서대로 저장해야하는데, 이때 고려되는 것이 바이트 저장 순서이다.

 

  2바이트 이상의 데이터는 메모리에 연속적으로 저장된다. 이때 각 바이트가 메모리에 정렬되는 방식을 바이트 오더링(Byte Ordering)이라고 부른다.

  바이트 오더링은 두 가지 방식으로 나눌 수 있고, 빅 엔디안(Big Endian)과 리틀 엔디안(Little Endian)이 있다. 어떤 바이트부터 낮은 주소에 저장되는지에 따라 두 방식을 구분한다. 이해를 돕기 위해, 왼쪽에 있는 바이트일수록 '크다'라고 표현하겠다.

  예를들어 0x01234567과 같은 데이터가 있을 때, 가장 왼쪽의 0x01=가장 큰 바이트, 가장 오른쪽의 0x67=가장 작은 바이트이다. 빅 엔디안은 큰 바이트부터 낮은 주소에 저장하며, 반대로 리틀 엔디안은 작은 바이트부터 낮은 주소에 저장한다. 숫자가 크다고 큰 바이트라는 착각은 하지 않길 바란다. 이것 때문에 엄청 꼬였다.

 

  

 

 

5-1) 빅 엔디안

  가장 왼쪽에 있는 바이트부터 메모리의 낮은 주소에 저장된다(큰 바이트 낮은 주소). 네트워크 상에서 데이터를 전송할 때는 빅 엔디안 방식을 따른다. 대표적으로 SPARC CPU에서 빅 엔디안을 사용하며, 우리가 평소에 숫자를 보는 방식과 같아 메모리 저장 순서대로 읽을 수 있고 이해하기 쉽다. 평소에 숫자를 보는 방식이라는 것은, 0x01234567이라는 데이터가 주어졌을 때,0x01234567 그대로 읽는다는 것이다.

 

  4바이트 16진수 0x01234567(2진수 0000 0001 0010 0011 0100 0101 0110 0111)을 메모리 주소 0x100에 저장한 결과를 함께 보며 빅 엔디안에 대해 알아보자.

 

 

 

5-2) 리틀 엔디안

  가장 오른쪽에 있는 바이트부터 메모리의 낮은 주소에 저장된다(작은 바이트 낮은 주소). 대표적으로 Intel x86-64 CPU에서 리틀 엔디안을 사용하는데, 대다수의 개인용 컴퓨터 및 서버 환경에서 x86-64 CPU 아키텍처를 사용하고 있으니 잘 알아두어야 한다.

  0x01234567이 0x67452301으로 읽힐 것이다. 즉 거꾸로 읽어야 한다. 이 때, 비트 순서는 거꾸로 읽지 않는다. 76이 아니라 67이라는 뜻이다.

 -> 빅 엔디안과 리틀 엔디안은 서로 데이터를 저장하는 방식이 다르기 때문에, 두 컴퓨터가 데이터를 주고 받는다면 문제가 발생 할 것이다. 네트워크를 통해 데이터를 주고 받을 때에는 빅 엔디안 방식으로 주고 받자 약속하며, 이것을 네트워크 바이트 순서(Network byte order)라고 한다. 그렇기 때문에, 위에서 언급한 인텔 기반 시스템에서 소켓 통신을 할 때 바이트 순서에 신경 써야 한다.

 

 

 

 

 

5-3) 바이트 오더링 예시

  정교함과 정확함이 필수인 해킹 분야에서, 데이터가 어떤 바이트 오더링으로 메모리에 저장되었는지 고려하는 것은 기본이다. 리버싱 분야에서 메모리에 저장된 값을 이용해 역연산을 수행하여 어떤 정답이 되는 값을 찾아내는 작업은 매우 흔하다. 이때 메모리에 저장된 값이 어떤 엔디안으로 저장되어 있는지를 고려하지 않으면, 전혀 다른 데이터로 혼동하여 올바른 역연상 결과를 얻을 수 없게된다.

  예를들어 위의 사진과 같이, 리틀 엔디안으로 저장된 0x01234567을 빅 엔디안으로 생각하고 0x76543210이라는 숫자로 다뤄버리면 전혀 다른 데이터를 가지고 역연산을 수행하는 꼴이 된다.

 

  현실에서 많은 개인용 컴퓨터와 서버 환경이 x86 아키텍처를 사용하고 있어, 리틀 엔디안에 친숙해지는 편이 좋다. 아래 예시를 통해 자세히 살펴보도록 하자. 아래 예시는 문자열과 16진수 정수를 메모리에 저장하는 C프로그램의 소스 코드이다. 각각 메모리에 저장된 값과 출력값을 직접 확인하여 리틀 엔디안 방식이 어떻게 적용되는지 살펴보자.

 

  여기서 A가 왜 10이 아니라 41이냐고 생각할 수 있다. 여기서 A는 16진수로 해석하면 안된다. 문자열을 바탕으로 출력하는 것 이기 때문에 아스키코드 A를 생각해야한다. A의 아스키 값이 41이다.

#include <stdio.h>
#include <stdlib.h>

int main(void) {
    char * str = "ABCD"; // 16진수: 41424344
	puts(str);	// 문자열 출력 결과: ABCD

    unsigned int num = 0;
    num = 0x41424344;
    printf("%x\n", num);  // 16진수 출력 결과: 41424344
  
    return 0;
}
//C코드

0x555555556004: 0x41    0x42    0x43    0x44
//문자열 출력 결과

str 변수 주소의 메모리를 1바이트씩 4바이트 출력한 결과물이다. 문자열을 메모리에 저장할 때는 바이트 오더링을 고려하지 않는다. 따라서 문자열 ABCD는 리틀 에디안 방식을 따르지 않고, 문자 순서 그대로 메모리에 저장된다

 

 

0x7fffffffe314: 0x44    0x43    0x42    0x41
//문자열이 아닌 데이터 출력 결과-16진수 정수

num 변수 주소의 메모리를 1바이트씩 4바이트 출력한 결과이다. 문자열이 아닌 데이터는 리틀 엔디안 방식으로 저장된다. 출력값을 보면, 작은 바이트 즉 D부터 낮은 메모리에 저장되는 것을 볼 수 있다. 메모리는 우리가 문장을 읽는 방향으로 높아진다.

 

 

 

 

 

 

 

 

 

6. 비트 연산

  피연산자를 2진수로 표현하여 비트 단위로 연산하는 것을 비트 연산이라고 한다. 비트 단위로 논리 연산을 수행하거나, 비트를 특정 값만큼 이동하는 시프트(shift)연산을 수행한다.

 

 

 

6-1) 논리 연산/ 논리 연산자

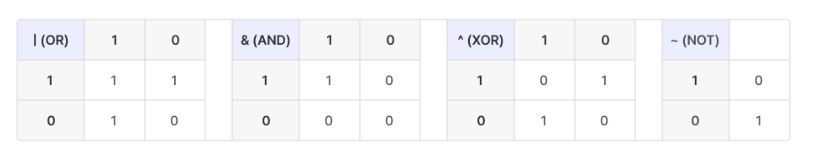
  참 또는 거짓 값으로 연산을 수행하고, 결과로 참(1,true) 또는 거짓(0,false)을 반환한다. 논리 연산자는 내가 아는 ||(or), &&(and), !(not)이 있다. 논리 연산표는 아래 그림과 같이 생겼다. 이건 잘했음 근데 왜 개론을 말아먹었는지 모르겠다

 

 

 

 

6-2) 비트 연산/ 비트 연산자

  비트 단위로 논리 연산을 수행한다. 1은 참, 0은 거짓을 나타낸다. 여기서 '비트 단위'가 의미하는게 뭔지 모를텐데 내가 이해시켜주겠다.  '비트 단위로 논리 연산을 수행한다'는 말은 비트 연산자가 각 비트를 개별적으로 처리하여 논리 연산을 수행한다는 것을 의미한다. 이는 각 비트가 독립적인 유닛으로 처리되어 해당 비트에 대한 연산이 수행된다는 것을 의미한다.

  예를 들어, 두 개의 8비트 숫자를 AND 연산하면, 각 비트에 대해 AND 연산이 수행되어 -> 새로운 8비트 숫자가 생성된다. 밑에 나오는 사진을 보면 이해가 될 것이다.

 

  비트 연산자에는  |(or), &(and), ^(XOR), ~(NOT)이 있다. 비트 연산은 아래 그림고 같이 진행된다. XOR은 두 비트가 달라야 참, 같으면 거짓이다. 비 동일성(베타적 논리합)을 구현한다. 또한 논리합은 OR을 의미하며, 논리 곱은 AND를 의미한다.

 

 

 

 

6-3) 시프트 연산자

  비트를 특정 값만큼 왼쪽 혹은 오른쪽으로 이동시킨다. n만큼 시프트한 결과는 2^n으로 곱하거나 나눈 값과 같다. 이해가 되지 않는게 당연하다. 밑에 예시를 보면서 이해해보자. 시프트 연산자에는 산술 시프트 x>>n, x<<n 그리고 논리 시프트 x>>>>n, x<<<<<n가 있다. 아래 사진과 함께 예시를 들어가며 이해해보자.

 

 

 

 

 

   먼저 왼쪽 시프트 연산을 살펴보자. 16비트 크기를 가지는 데이터 273을 왼쪽으로 4비트 만큼 시프트하는 과정을 볼 것이다. 273은 0b 0000 0001 0001 0001이다. 이를 4비트만큼 왼쪽으로 이동시키면, 0001 0001 0001 0000이 되고 273 ->4368이 된다.

  앞서 언급하였듯이 1비트 왼쪽으로 시프트하는 행위는 데이터에 2^1을 곱하는 것과 같다. 4비트 시프트 하였으므로 2^4를 곱하면 273 * 2^4 = 4368이 나오는 것을 알 수 있다.

 

 

 

 

  다음으로는 오른쪽 시프트 연산을 살펴보자. 2바이트, 즉 16비트 크기를 가지는 데이터 32529를 우측으로 4비트만큼 산술 시프트 하는 모습이다. 32529는 2진수로 0111 1111 0001 0001이다. 우측 산술 시프트는 MSB가 1이면 1로 채우고, 0이면 0으로 채운다. 양수면 양수 음수면 음수이므로 부호가 유지된다.  해당 데이터는 MSB가 0이므로 4비트만큼 우측 산술 시프트를 가하면 0000 0111 111 0001이다. 이는 데이터에  2^-4 를 곱하는 것과 같다.

 

 

 

 

  이제 논리 시프트 연산을 살펴보자. 왼쪽/ 오른쪽 논리 시프트 연산 모두 밀어낸 자리를 0으로 채운다. 따라서 이 경우 음수의 부호가 유지되지 않는다.

 

 

-----------<정리>----------

• 왼쪽 시프트: 숫자를 2의 거듭제곱으로 곱하는 효과가 있다
• 오른쪽 시프트: 숫자를 2의 거듭제곱으로 나누는 효과가 있다.

  시프트 연산은 곱셈이나 나눗셈 연산보다 훨씬 빠르기 때문에, 성능이 중요한 프로그램에서는 시프트 연산을 자주 사용한다. 효율적인 계산, 비트 마스킹(특정 비트의 값을 확인하거나 변경하는 데 사용), 데이터 압축 등 다양한 용도로 사용된다.

 

  또한 산술 산술시프트를 쓰면 되지 굳이 논리 시프트를....? 이라는 생각이 들수도 있다.내가 그랬다. 이유가 있으니 같은 출력값이 나와도 두 개로 구분되어 있을 것이다. 이건 밑에 활용 부분에서 이해할 수 있다.

#include <iostream>
using namespace std;

int main() {
    unsigned int x = 5;  // 5는 이진수로 0000 0101

    // 왼쪽 시프트
    unsigned int leftShift = x << 1;  // 결과: 0000 1010 (10)
    cout << "5 << 1 = " << leftShift << endl;

    // 오른쪽 시프트
    unsigned int rightShift = x >> 1;  // 결과: 0000 0010 (2)
    cout << "5 >> 1 = " << rightShift << endl;
}

 

 

 

 

 

 

 

 

 

 

7. 비트 연산 활용

  어떤 데이터가 존재할 때, 특정 위치의 비트만 표시하거나 가리는 연산을 비트 마스킹(Bit Masking)이라고 한다. 앞에서 살펴보았듯이 AND연산은 대응하는 비트가 모두 1이어야 1이 반환된다. 대응하는 비트중에 하나라도 0이면 0이된다. 이러한 AND연산의 특징을 활용한 비트 마스킹의 예시를 살펴보자.

  예를 들어 2바이트 크기의 데이터인 0xABCD가 존재할 때, AND연산을 활용하면 상위 8비트에 해당하는 0xAB는 없애고, 하위 8비트에 해당하는 0xCD만 남길 수 있다. 비트 마스킹보다 비트 바이트 용어가 더 헷갈린다...  이를 위해 0x00FF를 AND연산하면 된다.

 

 

 

7-1) AND 연산(&)과 시프트 연산을 활용하여 특정 비트/ 바이트 가져오기

  AND연산과 시프트 연산을 함께 활용하면 특정 위치의 비트를 가져올 수 있다. 32비트, 즉 4바이트 크기의 데이터인 0x12345678(0001 0010 0011 0100 0101 0110 0111 1000)에서 특정 비트만 가져오는 예시를 통해 살펴보자.

 

  하위 1바이트만 가져오기. 0x000000FF와 AND연산한다. 아직 시프트 연산은 사용하지 않았다

0x12345678 & 0x000000FF = 0x00000078 (0000 0000 0000 0000 0000 0000 0111 1000)

 

 

상위 1바이트만 가져오기.(12만 살린다는 뜻)

1. 우측으로 24번 논리 시프트를 수행한다

2. 24번 우측으로 산술 시프트한 후 0x000000FF와 AND연산한다.

3. 0x11000000과 AND연산한다 -> 특정 비트 패턴을 확인하는 용도로는 적합하지만, 바이트를 추출하는 데는 부적절하다. 특정 비트만을 확인하는 용도로는 사용 가능하다.

1. 0x12345678 >>> 24 = 0x00000012 (0000 0000 0000 0000 0000 0000 0001 0010)
2. 0x12345678 >> 24 & 0x000000FF = 0x00000012 (0000 0000 0000 0000 0000 0000 0001 0010)

 

 

상위에서두번째 바이트 가져오기(34만 살린다는 뜻)

1. 우측으로 16번 산술 시프트 후 0x000000FF와 AND연산한다 <- 이거 안보고 연습

0x12345678 >> 16 & 0x000000FF = 0x00000034 (0000 0000 0000 0000 0000 0000 0011 0100)

 

 

하위 1바이트의 상위 4비트 가져오기(7만 살린다는 뜻)

1. 우측으로 4번 산술 시프트 후 0x0000000F와 AND연산 <-이거 안보고 연습

0x12345678 >> 4 & 0x0000000F = 0x00000007 (0000 0000 0000 0000 0000 0000 0000 0111)

 

 

 

 

 

7-2) XOR 연산을 활용한 비교와 암호화

  XOR 연산은 비트 값이 같으면 0을 반환한다. 즉, 자기 자신과 XOR연산하면 결과는 0이다. 따라서 두 변수에 저장된 값끼리 XOR연산하여 결과가 0인지 확인하면 두 값이 같은지 비교할 수 있다.

 

  더 나아가서, 같은 값에 어떤 값을 2번 XOR하면 원래의 값과 동일해진다는 특성을 이용할 수도 있다. 예를들어 x ^ y =z일때, z ^ y = x ^ y ^ y = x이다. 이건 이해가 된다. 이러한 특성을 기반으로 y를 key로 설정하면 간단한 암호화, 복호화가 가능하다. 이 뒷 문장이 이해가 안된다.

 

 

 

 

7-3) 시프트 연산을 활용한 곱셈, 나눗셈

  앞에서 시프트 연산은 2^n을 곱하거나 나눈 결과와 동일하다는 것을 보았다.[7-2 다시 이해하자] 따라서 곱셈이나 나눗셈 연산자 대신 시프트 연산자를 사용하여 간단한 산술 연산을 수행할 수 있다. 시프트 연산자를 사용하면 비트 레벨에서 연산을 하므로 더 효율적이고 속도가 빠르다.

 

 

 

 

 

 

 

 

 

8. 인코딩, 디코딩

  인코딩(Encoding)은 데이터를 특정한 형식으로 변환하는 것을 말한다. 데이터의 크기를 줄이거나, 컴퓨터가 이해하기 쉽게 변환할 때 사용한다.

  인코딩된 데이터는 디코딩(Decoding)하여 원래의 값을 구할 수 있다. 인코딩은 암호화와 유사하지만 암호화는 데이터의 기밀성을 목적으로 남이 데이터를 알아보지 못하도록 변환하기 때문에 비밀키가 있어야 원문을 복구할 수 있지만, 인코딩은 누구나 표준화된 방식을 사용해서 디코딩하여 원문을 구할 수 있다는 점에서 차이가 있다. 실생활에서 볼 수 있는 인코딩의 예시로 압축이있다.

 

  어떤 인코딩된 데이터의 생김새를 보고 인코딩 방식을 유추하여 직접 디코딩해서 원문으로부터 단서를 얻어야 하는 경우도 있다. 이를 위해 자주 쓰이는 인코딩 방식과 각각의 형태를 알고 있으면 좋다

 

 

 

 

 

 

 

9. 아스키 코드, 유니코드

  컴퓨터는 0과 1만을 이용하여 정보를 처리하고 표현한다. 따라서 우리가 입력하는 모든 글자가 0과 1로 변환되려면 숫자로 표현되어야 한다. 이를 위한 것이 아스키코드(ASCII)이다. 아스키 코드는 정보 교환을 위한 미국 표준 코드로, 문자 -> 숫자로 변환하는 문자 인코딩의 표준이다.

  아스키 문자 1개는 1바이트 크기로, 7비트로 문자를 표현하고 1비트는 오류 체크를 위해 사용한다. 따라서 2^7=128가지의 문자 표현이 가능하며, 각 문자는 0~127까지의 10진수 값을 가진다.

 

 

 

  유니코드(Unicode)는 영어 뿐만 아니라, 전세계 모든 언어의 문자에 고유한 번호를 부여하는 국제 표준 코드이다. 서로 다른 언어를 사용할 때 문자가 호환되지 않는 문제를 해결하기 위하여 만들어졌다. 아스키 코드보다 용량을 크게 확장하여 최대 32비트로 문자 1개를 표현하여, 143000개 이상의 문자를 표현할 수 있다.

 

  UTF-8, UTF-16, UTF-32 등 유니코드를 사용하는 다양한 인코딩 형식이 존재한다. 이는 컴퓨터가 어떤 문자를 어떻게 읽어야 하는지 미리 정해준다. UTF 뒤의 숫자는 비트를 의미한다. 가장 일반적으로 사용되는 UTF-8은 1~4 바이트의 가변적인 크기로 문자 1개를 표현하는 방식으로, 아스키 코드와 유사하다. 현재 컴퓨터로 볼 수 있는 글자는 대부분 UTF-8로 인코딩된 값이다.

 

 

 

 

 

 

 

10. URL 인코딩(퍼센트 인코딩.인 이유는 내용 참조)

  웹에서 사용되는 URL은 특정한 형식의 문자열만 혀용한다. 알파벳 대/소문자, 숫자, 일부 특수 문자만을 포함할 수 있다. 웹 브라우저로부터 받은 URL 문자열을 유효한 형식으로 변환하는 것을 URL인코딩이라고 한다.

  URL 인코딩을 통해 문자열을 인터넷으로 전송 가능한 형식으로 변환한다. 이를 통해 전송 중에 문자가 수정되거나(=전송 과정에서 문자들이 특별한 의미를 가지게 되거나, 전송 프로토콜에서 잘못 해석될 가능성이 있다는 의미) 의도와 다르게 해석되는 것을 막을 수 있다. 허용되지 않은 문자= 인코딩이 필요한 특수문자에는 :/?#[]!()%공백 등이 있다.

 

  URL인코딩은 %기호 뒤에 해당 문자의 아스키 코드 16진수 값을 붙여 나타낸다. 퍼센트 인코딩인 이유. 예를들어 URL에 공백이 포함되는 경우 + 혹은 %20으로 변환된다. 여기서 %20이 URL인코딩 결과이다.

 

 

여기서 %2C=0x2c(16*2 + 12=44)는 ,를 의미하고 / %20=공백 /%21=! /%3A(16*3 + 10=58)=:/ %29=)이다. 예를들어, %29=)에서 29는 10진수가 아니라 16진수이므로 헷갈리지 말자.

문자열: Welcome, Dreamhack Beginners! :)
문자열 URL인코딩 결과: Welcome%2C%20Dreamhack%20Beginners%21%20%3A%29

 

 

 

 

 

 

 

 

11. base64 인코딩

  base64 인코딩은 이진 데이터를 아스키 문자로 구성된 텍스트로 변환하는 인코딩 방식이다. 128개의 아스키 문자 중,  64개의 아스키 문자가 인코딩에 사용되기 때문에 64진법(Base64)이라는 의미에서 이러한 이름이 붙여졌다. 이러한 64개의 아스키 문자는 알파벳 대소문자 52개 + 숫자 10개 + +/2개 =64개이다.

ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/
//총 64개

 

  base64 인코딩은 이진 데이터를 그대로 포함할 수 없이, 텍스트만 허용되는 환경에서 이진 데이터를 텍스트 형식으로 나타내기 위해 사용한다. 예를들어 이진 데이터인 이미지를 HTML 파일에 넣는 경우 base64로 인코딩해 넣을 수 있다.

(이진 테이터: 컴퓨터 시스템에서 사용되는 기본적인 데이터 형식으로 0과 1의 조합으로 표현된다. bit는 이진 데이터의 가장 기본 단위이며, 이진 데이터는 2진수 16진수 10진수로 표현된다.)

 

  -> 이진 데이터는 다양한 형태로 변환되어 전송되거나 저장된다. URL 인코딩이나 Base64인코딩과 같은 기법은 이진 데이터를 안전하게 전송하기 위해 사용된다.

 

 

 

  +여기 어렵다 집중하자. 왜 Z가 011001인가....?

 

 

 

 

--<실습>--------

  온라인 base64 디코더를 사용해서 다음의 데이터를 직접 디코딩 해보자! [ Base64 Decode and Encode - Online ]

 

 

 

 

 

 

 

* * * 추가적으로 공부가 필요하다고 생각되는 것/ 익숙하지 않은 것 * * * *

1. 인코딩

  1.1.  UTF-8, UTF-16, UTF-32 등

  1.2. URL인코딩, base64 인코딩

 

2. 데이터 비트 계산- 언제 4비트로 나누고 언제 2비트로 나누는지

 

 

* * * * 사용한 링크 * * * *

Base64 Decode and Encode - Online